Introduction

A wide variety of seismic waves propagate along the surface of the earth. They are called surface waves because their amplitude decreases exponentially with increasing depth. The Rayleigh wave is important in engineering studies because of its simplicity and because of the close relationship of its velocity to the shear-wave velocity for earth materials. As most earth materials have Poisson's ratios in the range of 0.25 to 0.48, the approximation of Rayleigh wave velocities as shear-wave velocities causes less than a 10% error. Rayleigh wave studies for engineering purposes have most often been made in the past by direct observation of the Rayleigh wave velocities. One method consists of excitation of a monochromatic wave train and the direct observation of the travel time of this wave train between two points. As the frequency is known, the wavelength is determined by dividing the velocity by the frequency.

The assumption that the depth of investigation is equal to one-half of the wavelength can be used to generate a velocity profile with depth. This last assumption is somewhat supported by surface wave theory, but more modern and comprehensive methods are available for inversion of Rayleigh-wave observations. Similar data can be obtained from impulsive sources if the recording is made at sufficient distance such that the surface wave train has separated into its separate frequency components.

Spectral Analysis of Surface Waves (SASW)

The promise, both theoretical and observational, of surface wave methods has resulted in significant applications of technology to their exploitation. The problem is twofold:

To determine, as a function of frequency, the velocity of surface waves traveling along the surface (this curve, often presented as wavelength versus phase velocity, is called a dispersion curve).

From the dispersion curve, determine an earth structure that would exhibit such dispersion. This inversion, which is ordinarily done by forward modeling, has been automated with varying degrees of success.

Basic Concept

Spectral analysis, via the Fourier transform, can convert any time-domain function into its constituent frequencies. Cross-spectral analysis yields two valuable outputs from the simultaneous spectral analysis of two time functions. One output is the phase difference between the two time functions as a function of frequency. This phase difference spectrum can be converted to a time difference (as a function of frequency) by use of the relationship:

(49)

where

If the two time functions analyzed are the seismic signals recorded at two geophones a distance d apart, then the velocity, as a function of frequency, is given by:

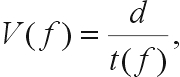(50)

where

If the wavelength (λ) is required, it is given by:

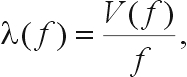(51)

As these mathematical operations are carried at for a variety of frequencies, an extensive dispersion curve is generated. The second output of the cross-spectral analysis that is useful in this work is the coherence function. This output measures the similarity of the two inputs as a function of frequency. Normalized to lie between 0 and 1, a coherency of greater than 0.9 is often required for effective phase difference estimates. Once the dispersion curve is in hand, the calculation-intensive inversion process can proceed. Although the assumption given above of depth equal to one-half the wavelength may be adequate if relatively few data are available, the direct calculation of a sample dispersion curve from a layered model is necessary to account for the abundance of data that can be recorded by a modern seismic system. Whether or not the inversion is automated, the requirements for a good geophysical inversion should be followed, and more observations than parameters should be selected.

Calculation methods for the inversion are beyond the scope of this manual. The model used is a set of flat-lying layers made up of thicknesses and shear-wave velocities. More layers are typically used than are suspected to be present, and one useful iteration is to consolidate the model layers into a geologically consistent model and repeat the inversion for the velocities only.

The advantages of this method are:

1. High frequencies (1-300 Hz) can be used, resulting in definition of very thin layers.
2. The refraction requirement of increasing velocities with depth is not present; thus, velocities that decrease with depth are detectable.

By using both of these advantages, this method has been used to investigate pavement substrate strength. An example of typical data obtained by an SASW experiment is shown in Figure 260. The scatter of these data is smaller than typical SASW data. Models obtained by two different inversion schemes are shown in Figure 261 along with some crosshole data for comparison. Note that the agreement is excellent above 20 m of depth.

Figure 260. Typical Spectral Analysis of Surface Waves data.

Figure 261. Inversion results of typical Spectral Analysis of Surface Waves data.

Data Acquisition

Most crews are equipped with a two- or four-channel spectrum analyzer, which provides the cross-spectral phase and coherence information. The degree of automation of the subsequent processing varies widely from laborious manual entry of the phase velocities into an analysis program to automated acquisition and preliminary processing. The inversion process similarly can be based on forward modeling with lots of human interaction or true inversion by computer after some manual smoothing.

A typical SASW crew consists of two persons, one to operate and coordinate the source and one to monitor the quality of the results. Typical field procedures are to place two (or four) geophones or accelerometers close together and to turn on the source. The source may be any mechanical source of high-frequency energy; moving bulldozers, dirt whackers, hammer blows, and vibrators have been used. Some discretion is advised as the source must operate for long periods of time, and the physics of what is happening are important. Rayleigh waves have predominantly vertical motion; thus, a source whose impedance is matched to the soil and whose energy is concentrated in the direction and frequency band of interest will be more successful.

Phase velocities are determined for waves with wavelength up to two times the distance between the geophones. Then the phones are moved apart, usually increasing the separation by a factor of two. Thus, overlapping data are acquired, and the validity of the process is checked. This process continues until the wavelength being measured is two to three times the required depth of investigation. Then the apparatus is moved to the next station where a sounding is required. After processing, a vertical profile of the shear-wave velocities is produced.

Advantages and Limitations

1. The assumption of plane layers from the source to the recording point may not be accurate.
2. Higher modes of the Rayleigh wave may be recorded. The usual processing assumption is that the fundamental mode has been measured.
3. Spreading the geophones across a lateral inhomogeneity will produce complications beyond the scope of the method.
4. Very high frequencies may be difficult to generate and record.

Multi-Channel Analysis of Surface Waves

The most common surface wave method today for geotechnical investigations is multi-channel analysis of surface waves (MASW). MASW typically uses a linear, L-shaped, or circular array of geophones (typically 24 or 48) for measuring the surface wave dispersion curve. The dispersion curve is then inverted to determine the corresponding shear wave velocity profile. MASW can be conducted with an active sound source similar to SASW, or using ambient noise. The method provides Vs information in either 1D (depth) or 2D (depth and surface distance) formats.

Basic Concept

Using an array of geophones connected to a multi-channel seismograph, seismic travel-times, amplitudes, and frequency of energy created by hammer blows to the ground surface is measured. As an alternative method, ambient seismic noise can also be recorded. Such noise, sometimes called microtremors, is constantly being produced by cultural and natural noise.

Because MASW processing schemes utilize a wavefield transform applied to the field data, the method has the capability to automatically account for adverse affects of near-field, far-field, spatial aliasing, and ambient energy. Therefore, acquisition parameters for MASW have a wide range of tolerance, unlike conventional refraction and reflection seismic surveys. The two most important parameters to be considered for MASW surveys are the source offset and the receiver spacing. These parameters are dependent on the site conditions and the average stiffness of the near-surface geologic materials.

The MASW method can be used to determine shear wave profiles to depths of up to 100 meters. However, due to the dispersive nature of surface waves with longer wavelengths penetrating deeper into the subsurface than shorter wavelengths, resolution decreases significantly with depth.

Data Acquisition

For a 2D investigation, the seismic equipment is laid out in an array very similar to that used in seismic refraction surveys. A multiple number of receivers (usually 24 or more) are deployed with an even spacing along a linear survey line with geophones connected to a multi-channel seismograph. Each channel is dedicated to recording vibrations from one receiver. Typically records of 1 second are stored in the seismograph from impacts to the surface repeated several times for signal stacking, using a 1 millisecond sample interval. One multichannel record, commonly referred to as a shot gather, consists of a multiple number of time series (called traces) from all the receivers in ordered manner (i.e., 1 through 24). When recording ambient noise, record time is typically 10-15 minutes. Since the equipment and setup is very similar to the one used for seismic refraction, it can often be beneficial to collect refraction and MASW data simultaneously.

Data Processing and Interpretation

The data is processed using one of several commercially available software packages. MASW interpretation requires no prior assumptions about the subsurface structure. Data processing is a complex series of iterative sequences combining shot gathers, analyzing each shot record for dispersion of the surface waves recorded, inverting the dispersion curve to 1D Vs profiles, and combining the 1D profiles into 2D cross sections. Figure 123 illustrates the process flow for analysis and interpretation of MASW data.

Figure 123. Illustration of the process used to derive MASW shear wave velocity (2D) cross-sections (from Kansas Geologic Survey).

If a 1D shear wave velocity profile is required then the 1D MASW method can be used. Figure 124 shows a shear wave profile with the ReMi results being compared with a shear wave velocity log. Such results may be useful for several applications including soil compaction control, pavement evaluation, maping the subsurface and estimating the strength of subsurface materials and finding buried cultural features such as dumps and piers.

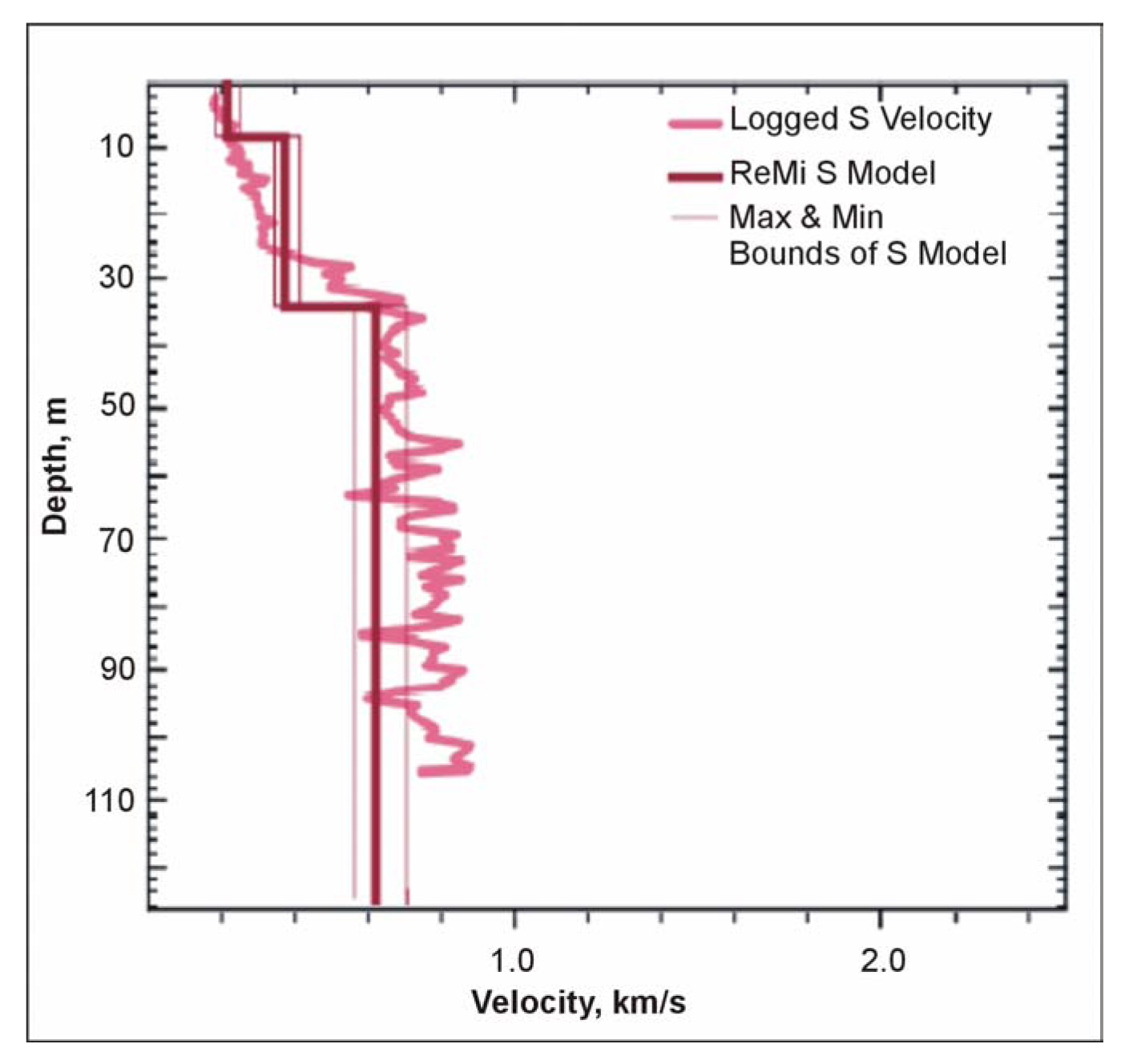
Figure 124. Figure 124. Shear-wave profile interpretation from a SeisOpt survey.

Advantages

The method is reported to have a wide range of applications, including rippability studies, void and utility detection, basement mapping and fault mapping. In addition, the 1D MASW method, which with the right setup can determine shear wave velocities to depths of 100 meters, can be used to determine the NEHRP soil classification at a site.

Limitations

Since the method is relatively new, the limitations may not yet be apparent. However, since the method partly relies on ambient noise, it is possible that all of the frequencies required for a particular target may not be present at a particular site. At some sites, such as near a busy highway, the frequencies may be dominated by a small range of frequencies having a high amplitude. Resolution decreases quickly with depth which limits the ability to detect thinner layers at depth.

Common-Offset Rayleigh Wave Method

This method is also called Common-Offset Surface Waves. The method is quite effective at mapping inhomogeneities in the near surface, although it is not a frequently used method. The field techniques are easy to apply, and compared to other seismic methods, it is a rapid technique.

This method uses Rayleigh waves to detect fracture zones and associated voids. Rayleigh waves, also known as surface waves, have a particle motion that is counterclockwise with respect to the direction of travel. Figure 262 illustrates the particle motion for Rayleigh waves traveling in the positive X direction. In addition, the particle displacement is greatest at the ground surface, near the Rayleigh wave source, and decreases with depth. Three shot points are shown, labeled A, B, and C. The particle motion and displacement are shown for five depths under each shot point. For shot B, over the void, no Rayleigh waves are transmitted through the water/air filled void. This affects the measured Rayleigh wave recorded by the geophones over the void. Four parameters are usually observed. The first is an increase in the travel time of the Rayleigh wave as the fracture zone above the void is crossed. The second parameter is a decrease in the amplitude of the Rayleigh wave. The third parameter is reverberations (sometimes called ringing) as the void is crossed. The fourth parameter is a shift in the peak frequency toward lower frequencies. This is caused by trapped waves, similar to a tube wave in a borehole. The effective depth of penetration is approximately one-third to one-half of the wavelength of the Rayleigh wave.

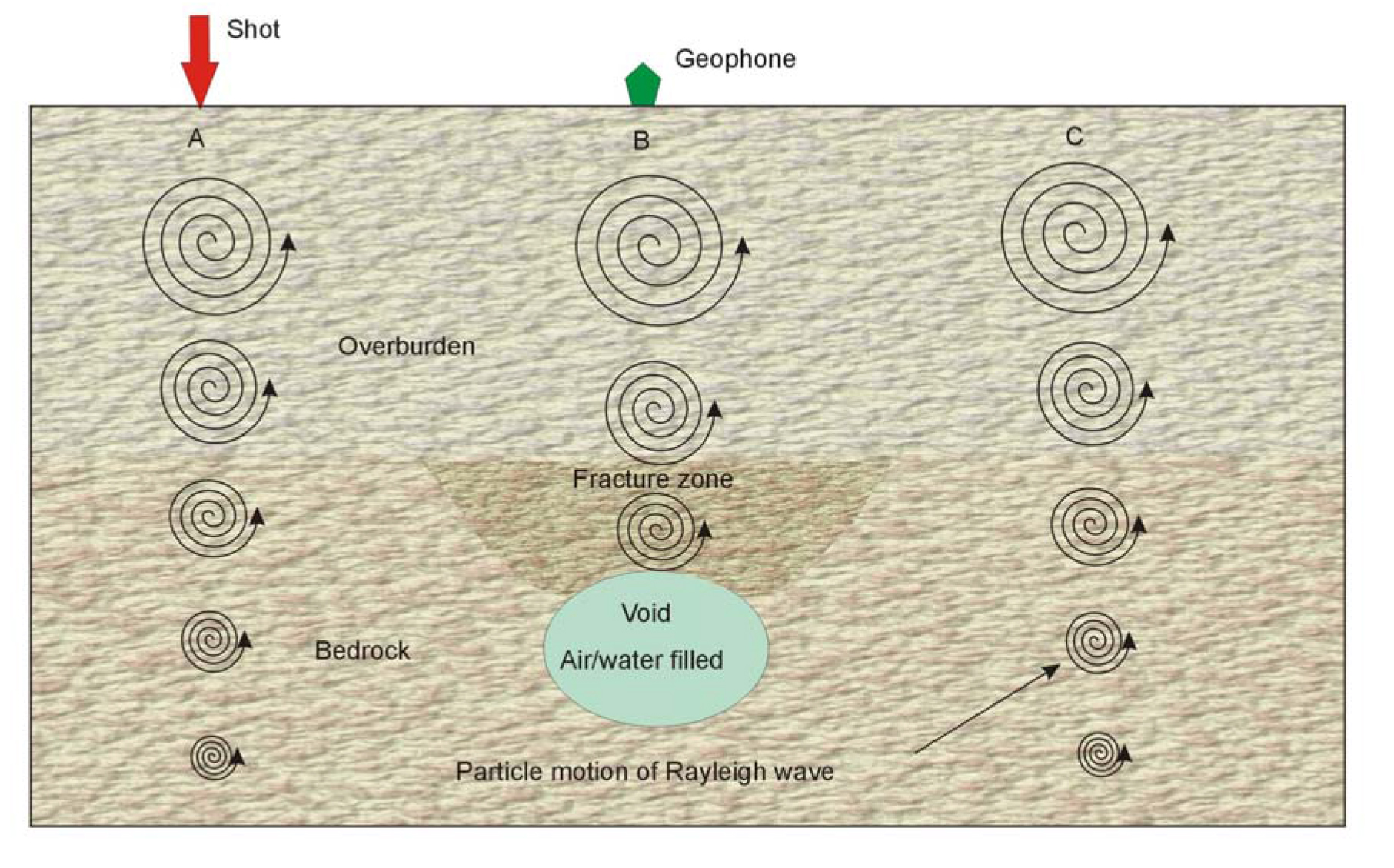
Figure 262. Rayleigh wave particle motion and displacement.

Rayleigh waves are created by any impact source. For shallow investigations, a hammer is all that is needed. Data are recorded using one geophone and one shot point. The distance between the shot and geophone depends on the depth of investigation and is usually about twice the expected target depth. Data are recorded at regular intervals across the traverse while maintaining the same shot geophone separation. The interval between stations depends on the expected size of the void/fracture zone and the desired resolution. Generally, in order to clearly see the void/fracture zone, it is desirable to have several stations that cross the area of interest. Figure 263 presents data from a common offset Rayleigh wave survey over a void/fracture zone in an alluvial basin. The geophone traces are drawn horizontally with the vertical axis being distance (shot stations).

The data may be filtered to highlight the Rayleigh wave frequencies and is then plotted as shown on Figure 263. Because the peak frequency of the seismic signal decreases over a void/fracture zone, a spectral analysis of the traces can assist in the interpretation of the data by highlighting the traces with lower frequencies. The data shown in Figure 263 illustrate many of the features expected over a void/fracture zone. The travel time to the first arrival of the Rayleigh wave is greater across the void/fracture and is wider than the actual fractured zone. The amplitudes of the Rayleigh waves decrease as the zone is crossed. In addition, the wavelength of the signals over the fracture/void is longer than those over unfractured rock, showing that the high frequencies have been attenuated. Since the records are not long enough, the ringing effect is not presented in these data.

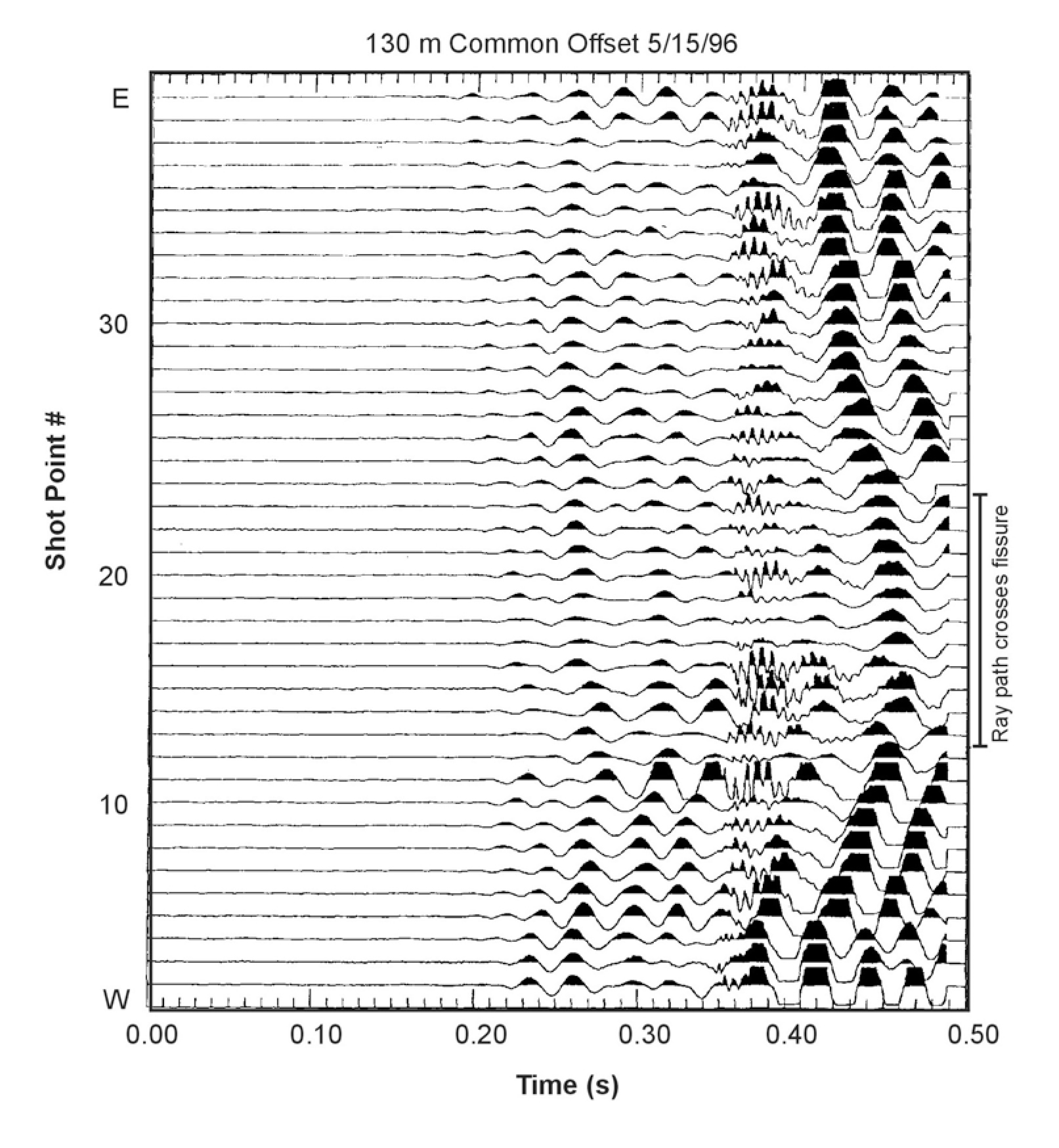
Figure 263. Data from a Rayleigh wave survey over a void/fracture zone.

Rayleigh waves are influenced by the shear strength of the rocks as well as fractures and voids, and changes in shear strength can cause anomalies similar to those obtained over these features. The depth of penetration and target resolution are influenced by the wavelengths generated by the seismic source. Since longer wavelengths, which have lower resolution, are needed to investigate to greater depths, fractures and voids at depth need to be increasingly larger in order to be observed. However, this method is faster and less costly than most other seismic methods.