Introduction
Seismic methods are the most commonly conducted geophysical surveys for engineering investigations. Seismic refraction provides engineers and geologists with the most basic of geologic data via simple procedures with common equipment.
Any mechanical vibration is initiated by a source and travels to the location where the vibration is noted. These vibrations are seismic waves. The vibration is merely a change in the stress state due to a disturbance. The vibration emanates in all directions that support displacement. The vibration readily passes from one medium to another and from solids to liquids or gasses and in reverse. A vacuum cannot support mechanical vibratory waves, while electromagnetic waves can be transmitted through a vacuum. The direction of travel is called the ray, ray vector, or ray path. Since a source produces motion in all directions the locus of first disturbances will form a spherical shell or wave front in a uniform material. There are two major classes of seismic waves: body waves, which pass through the volume of a material; and, surface waves, that exist only near a boundary.
Body waves. These are the fastest traveling of all seismic waves and are called compressional or pressure or primary wave (P-wave). The particle motion of P-waves is extension (dilation) and compression along the propagating direction. P-waves travel through all media that support seismic waves; air waves or noise in gasses, including the atmosphere. Compressional waves in fluids and gases (e.g., water and air), are commonly referred to as acoustic waves.
The second wave type is the secondary or transverse or shear wave (S‑wave). S-waves travel slower than P-waves in solids. S-waves have particle motion perpendicular to the propagating direction, like the obvious movement of a rope as a displacement speeds along its length. These transverse waves can only transit material that has shear strength. S-waves therefore do not exist in liquids and gasses, as these media have no shear strength.
S-waves may be produced by a traction source or by conversion of P-waves at boundaries. The dominant particle displacements are vertical for SV-waves traveling in a horizontal plane, while the dominant particle displacement is horizontal for SH-waves traveling in the vertical plane. SH-waves are often generated for S-wave refraction evaluations of engineering sites.
Elastic body waves passing through homogeneous, isotropic media have well-defined equations of motion. Most geophysical texts, including Grant and West (1965), include displacement potential and wave equations. Utilizing these equations, computations for the wave speed may be uniquely determined. Field surveys can readily obtain wave velocities, VP and VS; velocities are in units of length per time, usually meters/second (m/s). A homogeneous, isotropic medium's engineering properties of Young's or elastic modulus (E) and shear modulus (G) and either density (pb) or Poisson's ratio (ν) can be determined if VP and VS are known. The units of these measures are: moduli in pressure, usually pascals (Pa); density in mass per volume, grams/cubic meter (g/m3 = 10-6 mg/m3); and Poisson's ratio, ν, is dimensionless. Manipulation of equations from Grant and West (1965) yields
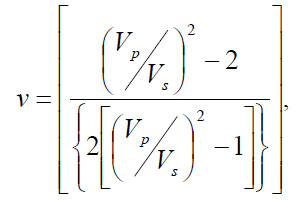 (41)
(41)
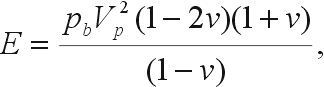 (42)
(42)
 (43)
(43)
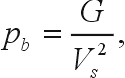 (44)
(44)
Note that these are not independent equations. Knowing two velocities uniquely determines only two unknowns of pb, ν, or E. Shear modulus is dependent on two other values. Poisson's ratio, ν, varies from 0.0 to a value less than 0.5 from Equations 41 and 42. For units at the surface, pb , the density, can be determined from samples, or for the subsurface from bore hole samples, or downhole logging. Estimates may be assumed for ν by material type. Usually the possible range of pb is approximated, and ν is estimated. Equations 41 through 44 may be compared to the approximate values with some judgment applied. Table 15 provides some typical values selected from Hempen and Hatheway (1992) for VP; Das (1994) for dry pb of soils; Blake (1975) for pb,dry of rock; and Prakash (1981) for ν. Other estimates of pb are contained in the section on gravity methods. Blake (1975) offers laboratory values of all these parameters, but field values will vary considerably from the lab estimates.
Surface waves. Two recognized vibrations, which exist only at "surfaces" or interfaces, are Love and Rayleigh waves. Traveling along a surface, these waves attenuate rapidly with distance from the surface. Surface waves travel slower than body waves. Love waves travel along the surfaces of layered media, and are most often faster than Rayleigh waves. Love waves have particle displacement similar to SH-waves. A point in the path of a Rayleigh wave moves back, down, forward, and up repetitively in an ellipse like ocean waves.
Surface waves are produced by surface impacts, explosions, and waveform changes at boundaries. Love and Rayleigh waves are also portions of the surface wave train in earthquakes. These surface waves may carry greater energy content than body waves. These wave types arrive last, following the body waves, but can produce larger displacements in surface structures. Therefore, surface waves may cause more damage from earthquake vibrations.
Table 15. Typical/representative field values of VP, pb and ν for various materials.

Wave theory. As a seismic disturbance moves away from a source location; the locus of points defining the expanding disturbance is termed the wavefront. Any point on a wavefront acts as a new source and causes displacements in surrounding positions. The vector normal to the wavefront is the ray path through that point, and is the direction of propagation. Upon striking a boundary between differing material properties, wave energy is transmitted, reflected, and converted. The properties of the two media and the angle at which the incident ray path strikes will determine the amount of energy reflected off the surface, refracted into the adjoining material, lost as heat, and changed to other wave types.
An S-wave in rock approaching a boundary of a lake will have an S-wave reflection, a P-wave reflection, and a likely P-wave refraction into the lake water (depending on the properties and incident angle). Since the rock-water boundary will displace, energy will pass into the lake, but the water cannot support an S-wave. The reflected S-wave departs from the boundary at the same angle normal to the boundary as the arriving S-wave struck. In the case of a P-wave incident on a boundary between two rock types (of differing elastic properties), there may be little conversion to S-waves. Snell's Law provides the angles of reflection and refraction for both the P- and S-waves. [Zoeppritz's equations provide the energy conversion for the body wave forms.] In the rock on the source side (No. 1), the velocities are VP1 and VS1; the second rock material (No. 2) has properties of VP2 and VS2. Then for the incident P‑wave (P1i), Snell's Law provides the angles of reflections in rock No. 1 and refraction in rock No. 2 as:
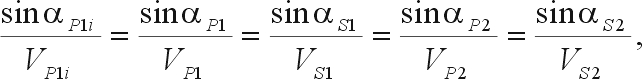 (45)
(45)
The second and third terms of equation 45 are reflections within material No. 1; the fourth and fifth terms are refractions into medium No. 2. Note that none of the angles can exceed 90 degrees, since none of the sin terms can be over 1.0, and αP1i = αP1.
Two important considerations develop from understanding equation 45. First is the concept of critical refraction. If rock No. 1 has a lower velocity than rock No. 2 or VP1 < VP2, then from Equation 45, sin αP2 > sin αP1i and the refracted αP2 > αP1i, the incident angle. Yet sin αP2 cannot exceed 1.00. The critical incident angle causes the refraction to occur right along the boundary at 90° from the normal to the surface. The critical angle is that particular incident angle such that sine αP2 = 1.0 and αP2 = 90 deg, or α(P1i)cr = sin-1(VP1/VP2). Secondly, any incident angle > α(P1i)cr from the normal will cause total reflection back into the source-side material, since sin αP2 ≯ 1.0. For the latter case, all the P-wave energy will be retained in medium No. 1.
Other wave phenomena occur in the subsurface. Diffractions develop at the end of sharp boundaries. Scattering occurs due to inhomogeneities within the medium. As individual objects shrink in size, their effect on scatter is reduced. Objects with mean dimensions smaller than one- fourth of the wavelength will have little effect on the wave. Losses of energy or attenuation occur with distance of wave passage. Higher frequency waves lose energy more rapidly than waves of lower frequencies, in general.
The wave travels outward from the source in all directions supporting displacements. Energy dissipation is a function of the distance traveled, as the wave propagates away from the source. At boundaries, the disturbance passes into other media. If a wave can pass from a particular point A to another point B, Fermat's principle states that the ray path taken is the one requiring the minimum amount of time. In crossing boundaries of media with different properties, the path will not be the shortest distance (a straight line) due to refraction. The actual ray path will have the shortest travel time. Since every point on a wavefront is a new source, azimuths other than that of the fastest arrival will follow paths to other locations for the ever-expanding wave.
Data Acquisition
Digital electronics have continued to allow the production of better seismic equipment. Newer equipment is hardier, more productive, and able to store greater amounts of data. The choice of seismograph, sensors(geophones), storage medium, and source of the seismic wave depend on the survey being undertaken. The sophistication of the survey, in part, governs the choice of the equipment and the field crew size necessary to obtain the measurements. Costs rise as more elaborate equipment is used. However, there are efficiencies to be gained in proper choice of source, number of geophone emplacements for each line, crew size, channel capacity of the seismograph, and requirements of the field in terrain type and cultural noise.
Sources. The seismic source may be a hammer striking the ground or an aluminum plate or weighted plank, drop weights of varying sizes, rifle shot, a harmonic oscillator, waterborne mechanisms, or explosives. The energy disturbance for seismic work is most often called the "shot," an archaic term from petroleum seismic exploration. Reference to the "shot" does not necessarily mean an explosive or rifle source was used. The type of survey dictates some source parameters. Smaller mass, higher frequency sources are preferable. Higher frequencies give shorter wavelengths and more precision in choosing arrivals and thereby estimating depths. Yet, sufficient energy needs to be transmitted to obtain a strong return at the end of the survey line. The type of source for a particular survey is usually known prior to going into the field. A geophysical contractor normally should be given latitude in selecting or changing the source necessary for the task. The client should not hesitate in placing limits on the contractor's indiscriminate use of some sources. In residential or industrial areas, perhaps the maximum explosive charge should be limited. The depth of drilling shot holes for explosives or rifle shots may need to be limited; contractors should be cautious not to exceed requirements of permits, utility easements, and contract agreements.
Geophones. The sensor receiving seismic energy is the geophone (hydrophone in waterborne surveys) or phone. These sensors are either accelerometers or velocity transducers, and convert ground movement into a voltage. Typically, the amplification of the ground is many orders of magnitude, but accomplished on a relative basis. The absolute value of particle acceleration cannot be determined, unless the geophones are calibrated.
Most geophones have vertical, single-axis response to receive the incoming waveform from beneath the surface. Some geophones have horizontal-axis response for S-wave or surface wave assessments. Triaxial phones, capable of measuring absolute response, are used in specialized surveys. Geophones are also chosen for their frequency band response.
The line, spread, or string of phones may contain one to scores of sensors depending on the type of survey. The individual channel of recording normally will have a single phone. Multiple phones per channel may aid in reducing wind noise or air blast or in amplifying deep reflections.
Seismographs. The equipment that records input geophone voltages in a timed sequence is the seismograph. Current practice uses seismographs that store the channels' signals as digital data at discrete time. Earlier seismographs would record directly to paper or photographic film. Stacking, inputting, and processing the vast volumes of data and archiving the information for the client virtually require digital seismographs. The seismograph system may be an elaborate amalgam of equipment to trigger or sense the source, digitize geophone signals, store multichannel data, and provide some level of processing display. Sophisticated seismograph equipment is not normally required for engineering and environmental surveys. One major exception is the equipment for sub-bottom surveys or nondestructive testing of pavements.
Data processing of seismic information can be as simple as tabular equations for seismic refraction. Processing is normally the most substantial matter the geophysicists will resolve, except for the interpretation.
A portion of the seismic energy striking an interface between two differing materials will be reflected from the interface. The ratio of the reflected energy to incident energy is called the reflection coefficient. The reflection coefficient is defined in terms of the densities and seismic velocities of the two materials as:
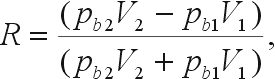 (46)
(46)
where
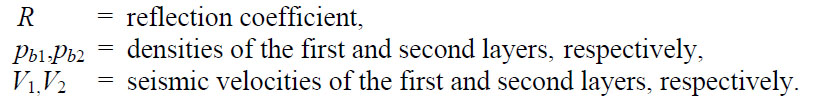
Modern reflection methods can ordinarily detect isolated interfaces whose reflection coefficients are as small as 0.02.